ஒரு எண்ணின் (அந்த எண்ணைத் தவிர) மற்ற வகுத்திகளின் கூட்டுத்தொகை அந்த எண்ணிற்கு சமமாக இருந்தால் அந்த எண் பூரண எண் (Perfect Number) எனப்படும்.

அந்த வகையில் மிகச் சிறிய பூரண எண் 6 (வகுத்திகள் 1,2,3) 6 = 1 + 2 + 3

அடுத்த பூரண எண் 28 (வகுத்திகள் 1,2,3,4,7,14) 28 = 1 + 2 + 3 + 4 + 7 + 14

பூரண எண்களைக் கண்டறிய ஒரு முறையை முதன் முதலில் யூக்ளிட் என்பவர் கண்டறிந்தார். அதாவது (2^n) -1 என்பது பகா எண்ணாக (Prime Number) இருந்தால் 2^(n-1) * ((2^n)-1) என்பது எப்பொழுதும் இரட்டைப் படை பூரண எண்ணைத் தரும். ஏறக்குறைய 2000 ஆண்டுகள் கழித்து ஆய்லர் என்பவர் இந்த சூத்திரத்தால் அனைத்து இரட்டைப்படை பூரண எண்களையும் கணக்கிட முடியும் என நிரூபித்தார்.

எனினும், இது வரை ஒரு ஒற்றைப் படை பூரண எண் கூடக் கண்டறியப் படவில்லை. ஒற்றைப்படை பூரண எண் இருக்கமுடியாது என்பதும் இதுவரை நிரூபிக்கப்படவில்லை.

நீங்கள் கண்டறிங்களேன்.

இந்தப் பூரண எண்களுக்கென்று சில புதிரான குண நலன்கள் உள்ளன. அனைத்துப் பூரண எண்களுமே 1+2+3+4+... என்ற தொடர் கூட்டலின் ஒரு பகுதியே!

உதாரணம்:

1+2+3 = 6

1+2+3+4+5+6+7 = 28

6ஐத் தவிர மற்ற அனைத்துப் பூரண எண்களையும் 1^3 + 3^3 + 5^3+... என்ற தொடர் கூட்டலின் ஒரு பகுதியாக எழுத முடியும்.

உதாரணம்: 1^3 + 3^3 = 28

ஒவ்வொரு பூரண எண்ணின் (6 ஐத்தவிர) இலக்க மூலம் (Digital Root) எப்போதும் 1 ஆகத் தான் இருக்கும்.

உதாரணம்: 28
2 + 8 = 10
1 + 0 = 1

496
4 + 9 + 6 = 19
1+9 = 10
1 + 0 = 1

சில பெரிய்ய்ய்ய்ய்ய பூரண எண்களையும் காண்போம்.

இது வரை கண்டறிந்ததிலேயே மிகப் பெரிய பூரண எண் (2^756838 * ((2^756839) -1).

இந்த எண் 4,55,663 இலக்கங்கள் உடையது!

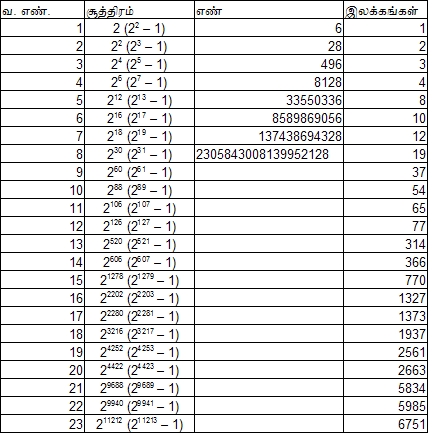
இதோ பூரண எண்களின் அட்டவணை!

கணினியால் கூட யூகிக்க முடியாத எண்ணைக் கண்டறிவதன் அவசியம் தற்போது வந்துள்ளது எண் கையெழுத்தினால். (Digital Signature).

RSA அல்காரிதத்தின் படி ஒரு பகா எண்ணை எடுத்து அதன் மூலம் இரு வெவ்வேறு சாவிகள் உருவாக்கி ஒன்றை அனுப்புபவரிடமும் இன்னொன்றை பெறுபவரிடமும் கொடுக்கிறார்கள். இதுவே டிஜிட்டல் கையெழுத்து. அந்தப் பகா எண்ணை யூகிக்க முடிந்தால்? அவ்வளவு தான்! கோடிக்கணக்கில் பணம் போயே போய் விடும்.

எனவே இது போன்ற எண்களின் பண்புகள், ஒரு எண்ணை வைத்து அடுத்த எண்ணினைக் கண்டறிய முடியுமா முடியாதா? என்பது போன்ற ஆராய்ச்சிகளுக்கு எல்லையும் இல்லை, மதிப்புக்கும் அளவு இல்லை.